Michael Wuerth's blog

Abstract

Representing an NP-complete problem as complex numbers led to the insight to use complement sets to solve NP-complete problems in P time. This technique of complement sets solves a problem in the NP class of languages in P time when the intersection of complement sets is used to identify the decisions in a problem to avoid when solving a NP problem. Therefore, this paper will solve the NP-complete problem of finding the maximum clique in a graph in linear time O(V + E) when the symmetric difference of complements sets is used to identify the valid members of the maximum clique, where V = number of vertices in a graph and E = number of edges in a graph. When this paper solves the maximum clique problem in deterministic polynomial time O(V + E), it will be proved that P = NP. Using this technique of complement sets, this paper will solve the halting problem because it can now be determined if a Turing Machine halts or doesn’t halt.

Keywords: P = NP, maximum clique problem.

The challenge
Determining the maximum size of a clique in a graph takes an exponential amount of time. This fact asks the question: is there a way to determine the maximum size of a clique in a graph in deterministic polynomial time? This paper answers the question with “Yes” and will provide a technique on how to do that proving that P = NP.

P, NP and complex numbers

Define class P of languages by
P = {L | L = L(M) for some Turing Machine M} [1]

Define class NP of languages by the condition that a language L over ∑ is in NP iff there is k ∈ N and a polynomial-time checking relation R such that for all w ∈ ∑*
w ∈ L <=> ∃y(|y| <= |w|k and R(w, y)}
where |w| and |y| are the lengths of w and y. [1]

A decision problem is a computational problem that can be posed as a yes-no question of the input values. A decision corresponds to an action that can be taken in a Turing machine. Nondeterministic decisions have more than one possible action that can be performed for a given situation. Deterministic decisions have only one action that can be performed for any given situation.

NP behavior, or nondeterministic polynomial behavior, is the set of decisions that are represented by the real dimension of a complex number a + bi. These decisions are examined by an algorithm to solve a problem in nondeterministic polynomial time. NP behavior requires all of the consequences of a decision to be examined to determine if the decision helps solve the problem.

P behavior, or deterministic polynomial behavior, is the set of decisions that are represented by the imaginary dimension of a complex number a + bi. These decisions are examined by an algorithm to solve a problem in deterministic polynomial time. P behavior requires the one consequence of a decision to be examined to determine if the decision helps solve the problem.

Let the real dimension of a complex number a + bi represent the set of decisions in a problem that are examined by an algorithm in nondeterministic polynomial time. Let the imaginary dimension of a complex number a + bi represent the set of decisions in a problem that are examined by an algorithm in deterministic polynomial time. Rotate the complex number a + bi so it represents the set of decisions that result after reducing a problem by eliminating invalid states. Then the conjugate a – bi represents the set of decisions that result after reducing a problem by eliminating valid states. Eliminating invalid states makes the problem easier to solve by examining only the decisions with valid states instead of examining every decision in the problem. Likewise, eliminating valid states makes the problem easier to solve by examining only the decisions with invalid states instead of examining every decision in the problem.

Let the complex number a + bi represent the set of decisions that result after reducing a problem by eliminating invalid states. Then the conjugate a – bi represents the set of decisions that result after reducing a problem by eliminating valid states. Eliminating invalid states makes the problem easier to solve by examining only the decisions with valid states instead of examining every decision in the problem. Likewise, eliminating valid states makes the problem easier to solve by examining only the decisions with invalid states instead of examining every decision in the problem.

Let the imaginary dimension b of the complex number a + bi and its conjugate a – bi represents the set of decisions with P behavior, the set of decisions that require the one consequence of a decision to be examined to determine if the decision helps solve the problem. Then the real dimension a of the complex number a + bi and its conjugate a – bi represents the set of decisions with NP behavior, the set of decisions that require all consequences of a decision to be examined to determine if the decision helps solve the problem.

The intersection of the set of valid states and the set of invalid states identifies decisions to avoid while solving the problem because the intersections contains states with NP behavior. The P = NP theorem later in this paper solves the maximum clique problem in linear time O(n) by identifying the intersection of the set of valid states and the set of invalid states so only P behavior in the problem remains.

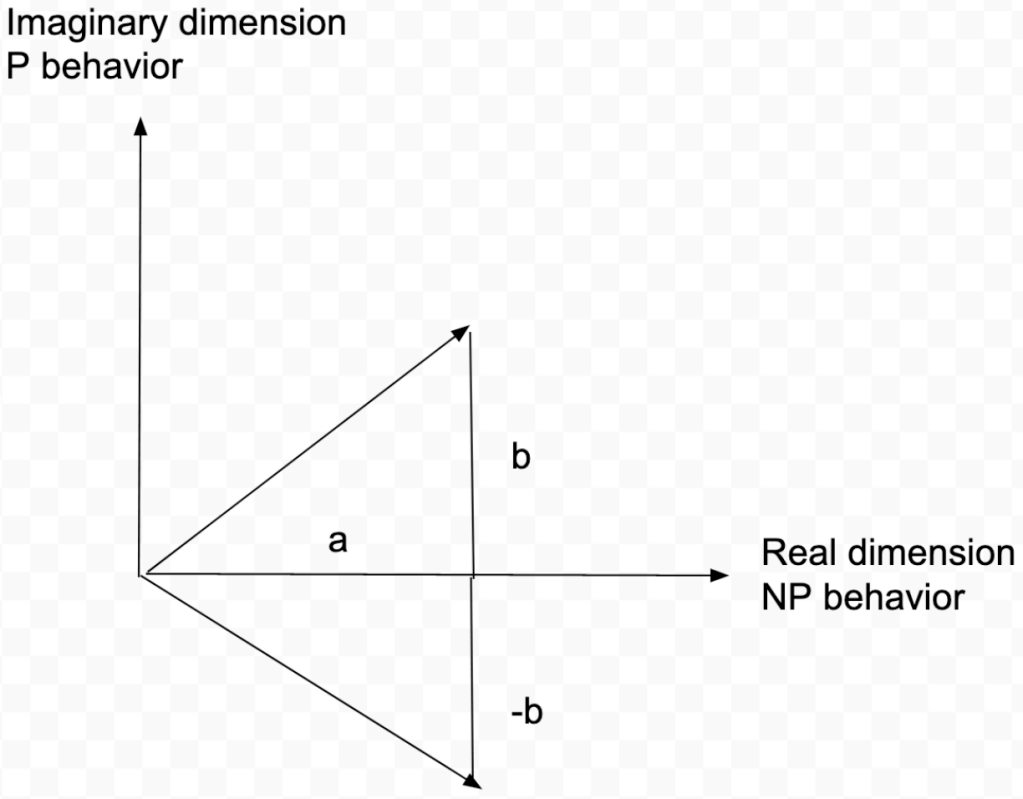
The real dimension a, the NP behavior, is what the complex number and its conjugate have in common.

The goal
Show how a NP problem can be solved in deterministic polynomial time.
A way to solve the problem of determining whether there is a clique of a given size in a graph in deterministic polynomial time will be shown by creating a way in polynomial time to avoid all NP behavior in problems when examining decision while solving the problem. When determining if a clique of a given size exists in a graph, NP behavior requires all of the consequences of all decisions—all combinations of possible elements to be added to a clique—to be examined to determine if a clique of a given size exists in a graph. Avoiding all NP behavior will leave only decisions involving P behavior when solving problems, meaning only a deterministic polynomial number of decisions, need to be examined to determine if a clique of a given size exists in a graph. When it is shown in this paper how to solve in deterministic polynomial time whether there is a clique of a given size in a graph, it will be shown how to solve the maximum clique problem in deterministic polynomial time. This will show that all problems in NP can also be solved in deterministic polynomial time, proving that P = NP.

Lemma 1
When a problem is reduced by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one (a polynomial-time reduction that results in deterministic polynomial in number) decision, the set of decisions represented by the imaginary dimension of a complex number results in only P behavior of the problem to be added to the imaginary dimension of the complex number. The set of decisions represented by the real dimension of a complex number will still contain NP behavior of the problem.

Proof of Lemma 1
By contradiction.
Start with all NP behavior in a problem being represented by the real dimension of the complex number a + bi. The imaginary dimension will never contain NP behavior. This is trivially true before the problem is reduced since initially a complex number with an imaginary dimension component of 0 does not have an imaginary component. Reduce the problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one (deterministic polynomial in number) decision p to be made.

Removing invalid states from the problem makes the problem easier to solve because the consequences of decisions with invalid states do not need to be examined to determine whether or not the consequence of a decision with invalid states solves the problem. Likewise, removing valid states from the problem also makes the problem easier to solve because the consequences of decisions with valid states do not need to be examined to determine whether or not the consequence of a decision with valid states solves the problem.

At each point in the reduction of the problem, a choice involving many decisions to be made is replaced with a choice that has only one (deterministic polynomial in number) decision p to be made. Add the decision p to the set of P decisions corresponding to the imaginary component of the complex number and remove the decision p from the set of NP decisions that contain choices involving many decisions to be made to solve the problem. The real component of the complex number corresponds to the set of NP decisions that could not be eliminated from the problem. This is how the NP behavior of the problem is reduced.

Contradiction: Suppose that decision p involved a nondeterministic polynomial number of decisions to be made. If this decision p was added to the set of P decisions then it would violate the condition that the set P has only elements containing decisions with only a deterministic polynomial number of decisions to be made. This contradicts the assumption that only P behavior is added to the imaginary dimension so Lemma 1 is proved.

Lemma 2
If set Z represents the complex number a + bi that represents a problem after the problem is reduced by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number) and set Z* represents the conjugate a – bi of the complex number that represents set Z, then the elements in set Z and set Z* are complement sets of each other.

Proof of Lemma 2
By construction.
Start with all NP behavior on the real axis of the complex number a + bi. This results in b = 0 in the complex number. Create two sets Z and Z* that are initially set to the empty set. Reduce the problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number). By Lemma 1, the set of decisions represented by the imaginary dimension of a complex number results in only P behavior of the problem to be added to the imaginary dimension of the complex number and the set of decisions represented by the real dimension of a complex number will still contain NP behavior of the problem. Adding decisions to the imaginary dimension of a complex number rotates the complex number counter clockwise towards the imaginary axis so the imaginary component of the complex number contains P behavior. The complex number now represents decisions with P behavior that replaced some of the decisions with NP behavior and the decisions with NP behavior that could not be eliminated from the problem. The complex number a + bi represents an algorithm that eliminates b decisions from a problem–thereby increasing the P behavior of the problem.

Let G = the set of all decisions in a problem. Before the problem is reduced, G contains all of the NP behavior in the problem.
Let G = {X_npi, X_npi+1, … X_npn}
where npi >= 1 and npi <= n and X_npi is one of the decisions in the problem that has NP behavior
G is represented by the complex number a + bi that initially has i = 0 so a + bi = a + 0 = a.

When reducing the problem, a choice involving many decisions to be made is replaced with a choice p that has only one (deterministic polynomial in number) decision to be made. Add the decision p as an element of the set Z. By Lemma 1, set Z will contain only P behavior in a problem. For each decision p that was added to set Z, add a decision that has the opposite, meaning complement, type of decision to set Z. Sets Z and Z* are now complement sets of each other because for each decision p added to set Z there will be a decision having the opposite, meaning complement, type of decision added to set Z*.

Let set Z be represented by the complex number that represents G after the complex number is rotated. Now i is nonzero so Z is represented by the complex number a + bi.
Let set Z (P behavior) = {ev_i, ev_i+1, … ev_a}
where i >=1 and i <= n and by Lemma 1 ev_i is one of the decisions of the problem that has P behavior with valid states. ev_a is the last element of set Z where a is number of elements with decisions that have P behavior with valid states.

Z represents some, not all, of the NP behavior that was eliminated from the problem by the complex number a + bi and the P behavior that was added by eliminating invalid states. Set Z contains elements that are the decisions with valid states so set Z reduces the problem because the consequences of decisions with invalid states do not need to be examined to determine whether or not the answer to a decision with invalid states solves the problem.

Conjugates of complex numbers
By Lemma 1, the imaginary dimension of a complex number a + bi represents the P behavior of the problem. The conjugate of the complex number a + bi is a – bi. Therefore, the imaginary dimension of the complex number a + bi represents P behavior that was added to the problem by eliminating invalid states and its conjugate a – bi represents P behavior that was added to the problem by eliminating valid states. The set of decisions represented by the complex number a + bi and its conjugate a – bi are the complement of each other because they are logically opposite of each other but they are still related to the original problem.

Let set Z* be represented by the conjugate a – bi of the complex number that represents set Z.
Let set Z* (P behavior) = {ei_i, ei_i+1, … ei_c}
where i >=1 and i <= n and by Lemma 1 ei_i is one of the decisions of the problem that has P behavior with invalid states. ei_c is the last element of set Z* where c is number of elements with decisions that have P behavior with invalid states.

Z* represents some, not all, of the NP behavior that was eliminated from the problem by the complex number a – bi and the P behavior that was added by eliminating valid states. Set Z* contains elements that are the decisions with invalid states so set Z* reduces the problem because the consequences of decisions with valid states do not need to be examined to determine whether or not the answer to a decision with valid states solves the problem.

Valid states = no conflict = Z
Invalid states = conflict = Z*

Because the elements in set Z* are the opposite, meaning complement, of the elements in set Z, Lemma 2 is proved.

Lemma 3
When complex numbers have the real axis represent the NP behavior of the problem and the imaginary axis represent the P behavior of the problem, the symmetric difference of complement sets results in only P behavior to be in the set of decisions that remains after a problem is reduced to its complement sets.

Proof of Lemma 3
By construction.
In this paper, complex numbers have the real axis represent the NP behavior of the problem and the imaginary axis represent the P behavior of the problem. Therefore, before the problem is reduced the problem has all NP behavior, no P behavior, which means all of the consequences of the decisions need to be examined to determine if the decisions help solve the problem. This means before the problem is reduced, the complex number a + bi has no imaginary component, i = 0, so the complex number that represents the problem a + bi = a + 0 = a.

Rotate the complex number a + bi that represents a problem counter clockwise by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number). The imaginary component of the complex number is now nonzero. By Lemma 1, some NP behavior is now eliminated from the algorithm and the P behavior of the problem is increased. By Lemma 1, only P behavior is contained in the imaginary dimension of the complex number a + bi so let set Z represent the set of decisions with P behavior that result from rotating the complex number a + bi.

Let G = the set of all decisions in a problem. Before the problem is reduced, G contains all of the NP behavior in the problem.
Let G = {X_npi, X_npi+1, … X_npn}
where npi >= 1 and npi <= n and X_npi is one of the decisions in the problem that has NP behavior.
G is represented by the complex number a + bi. i = 0 so a + bi = a + 0 = a.

Let set Z be represented by the complex number that represents G after the complex number is rotated. Now i is nonzero so Z is represented by the complex number a + bi.
Let set Z (P behavior) = {ev_i, ev_i+1, … ev_a}
where i >=1 and i <= n and by Lemma 1 ev_i is one of the decisions of the problem that has P behavior with valid states. ev_a is the last element of set Z where a is number of elements with decisions that have P behavior with valid states.

Z represents some, not all, of the NP behavior that was eliminated from the problem by the complex number a + bi and the P behavior that was added by eliminating invalid states. Set Z contains elements that are the decisions with valid states so set Z reduces the problem because the consequences of decisions with invalid states do not need to be examined to determine whether or not the answer to a decision with invalid states solves the problem.

Let Z* be represented by the conjugate a – bi of the complex number that represents set Z.
Let set Z* (P behavior) = {ei_i, ei_i+1, … ei_c}
where i >=1 and i <= n and by Lemma 1 ei_i is one of the decisions of the problem that has P behavior with invalid states. ei_c is the last element of set Z* where c is number of elements with decisions that have P behavior with invalid states.

Z* represents some, not all, of the NP behavior that was eliminated from the problem by the complex number a – bi and the P behavior that was added by eliminating valid states. Set Z* contains elements that are the decisions with invalid states so set Z* reduces the problem because the consequences of decisions with valid states do not need to be examined to determine whether or not the answer to a decision with valid states solves the problem.

Set Z* is the complement set of set Z so set Z* represents the set of decisions represented by the conjugate a – bi.

The symmetric difference
Set Z represents the rotated complex number a + bi and set Z* represents the conjugate a – bi so set Z and set Z* have a, the real dimension of the complex numbers, in common. The imaginary dimensions of the complex numbers represent the P behavior of the problem. The real dimensions of the complex numbers represents the NP behavior of the problem. Therefore, set Z and set Z* have the NP behavior of the problem in common. Set Z and set Z* have NP behavior in common when an element ev_i in set Z is the same as an element ei_i in set Z*. This is the key point that will be demonstrated in Lemma 4.

The real dimension a, the NP behavior, is what the complex number represented by set Z and its conjugate represented by set Z* have in common.

Need to construct: A way is needed to remove the NP behavior that is in common with the complement sets Z and Z* so only the P behavior remains.

Solution: The symmetric difference of complement sets removes what the complement sets have in common. Set Z represents the rotated complex number a + bi and set Z* represents the conjugate a – bi of set Z. The set of decisions represented by the conjugate a – bi represents the complement of the set of decisions that are represented by the rotated complex number a + bi because the set of decisions represented by the complex number and its conjugate are the logically opposite of each other but they are still related to the original problem. Set Z and set Z* have the real dimension that represents the NP behavior of the problem in common. Therefore, the symmetric difference of the sets of decisions represented by the complement sets Z and Z* result in only the P behavior of the problem to remain which is represented by the imaginary dimension.

Set Z has P behavior with valid states: {ev_i, ev_i+1, … ev_a}
Set Z* P behavior with invalid states: {ei_i, ei_i+1, … ei_c}
where i >=1 and i <= n.

Let set S be the symmetric difference of the complement sets Z and set Z*.

Let set S = (Z \ Z*) U (Z* \ Z)
Let set S = {ev_i, ev_i+1, … ev_a} \ {ei_i, ei_i+1, … ei_c} U {ei_i, ei_i+1, … ei_c} \ {ev_i, ev_i+1, … ev_a}
where i >=1 and i <= n.
Let set S = {ev_i, ev_i+1, … ev_a} U {ei_i, ei_i+1, … ei_c}
Let set S = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c}

The key point

Set S is the symmetric difference of the complement sets Z and Z* so set S only contains P behavior. The symmetric difference eliminates elements in sets Z and Z* when ev_i = ei_i. This is the key point that will be described in Lemma 4 in this paper.

Let S = {{ev_i, ei_i} ∈ {(Z \ Z) U (Z \ Z)} : ev_i ≠ ei_i}
Then NP behavior is eliminated from S and only P behavior remains in S.

Set S is the symmetric difference of set Z and set Z*. Set S results in only P behavior to be in the set of decisions that remains after a problem is reduced by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number) so Lemma 3 is proved.

Corollary 1
Valid or invalid states can be removed from the symmetric difference in deterministic polynomial time, linear time O(n).

Proof of Corollary 1
By direct proof.
By Lemma 3, after a problem is reduced to its complement sets the symmetric difference set S contains only P behavior. Because each element in set S has P behavior, only one decision needs to be examined for an element in set S to determine if the element in set S can be removed from the symmetric difference. However, the P behavior that remains in set S contains elements with complement states like valid and invalid states.

When the invalid states in set Z* are removed from set S, the decisions with the desired states, valid states, are the only decisions that will remain in the symmetric difference. Likewise, when the valid states in set Z are removed from set S, the decisions with the non desired states, invalid states, are the only decisions that will remain in the symmetric difference.

Desired elements
Set Z has P behavior with valid states: {ev_i, ev_i+1, … ev_a}

Set Z* P behavior with invalid states: {ei_i, ei_i+1, … ei_c} where i >=1 and i <= n.

Set S = the symmetric difference of Z and Z*

By Lemma 3, set S = (Z \ Z*) U (Z* \ Z) = P behavior only

Set S = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c}

Let set D (desired elements) = symmetric difference – invalid states

D = S – (invalid states)

D = S – Z*

D = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c} – {ei_i, ei_i+1, … ei_c} where i >=1 and i <= n.

D = {ev_i, ev_i+1, … ev_a}

Because set D is a subset of set S, the symmetric difference, by Lemma 3 set D contains only P behavior. Set D (desired elements) contains only valid states from the symmetric difference S. Because set D has only P behavior, set D can be searched in deterministic polynomial time, linear time O(n).

Not desired elements
Set Z has P behavior with valid states: {ev_i, ev_i+1, … ev_a}

Set Z* P behavior with invalid states: {ei_i, ei_i+1, … ei_c} where i >=1 and i <= n.

Set S = the symmetric difference of Z and Z*

By Lemma 3, set S = (Z \ Z*) U (Z* \ Z) = P behavior only

S = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c}

Let set ND (not desired elements) = symmetric difference – valid states

ND = S – (valid states)

ND = S – Z

ND = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c} – {ev_i, ev_i+1, … ev_a} where i >=1 and i <= n.

ND = {ei_i, ei_i+1, … ei_c}

Because set ND is a subset of set S, the symmetric difference, by Lemma 3 set ND contains only P behavior. Set ND (not desired elements) contains only invalid states from the symmetric difference S. Because set ND has only P behavior, set ND can be searched in deterministic polynomial time, linear time O(n). Therefore, Corollary 1 is proved.

Lemma 4
The problem of determining whether there are valid direct relationships in a clique in a graph can be solved in deterministic polynomial time when using complex numbers and the symmetric difference of complement sets to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number).

Proof of Lemma 4
By construction.

The steps in the proof are: use Lemma 2 to set up the complement sets, use Lemma 3 to calculate the symmetric difference of the complement sets, then use Corollary 1 to remove elements with invalid states. In this context, invalid states are elements from the symmetric difference that are not an ally of any other element in the candidate clique.

By Lemma 2, a problem is reduced by eliminating invalid states.

Valid states = no conflict = set Z
{ev_i, ev_i+1, … ev_a} = no conflict = set Z
where i >=1 and i <= n.
The letter v in ev_i represents only valid states which are represented where ev_i is one of the decisions of the problem that has P behavior with valid states. ev_a is the last element in set Z where a is number of elements meaning decisions in set Z that have P behavior with valid states in the set Z. By Lemma 1 ev_i is one of the decisions of the problem that has P behavior with valid states.

By Lemma 2, a problem is also reduced by eliminating valid states.

Invalid states = conflict = set Z*
{ei_i, ei_i+1, … ei_c} = conflict = set Z*
where i >=1 and i <= n.
The letter i in ei_i represents invalid states. Invalid states are represented where ei_i is one of the decisions of the problem that has P behavior with invalid states. ei_c is the last element in set Z* where c is number of elements meaning decisions in set Z* that have P behavior with invalid states. By Lemma 1, ei_c is one of the decisions of the problem that has P behavior with invalid states.

By Lemma 2 set Z* is the complement of set Z.

The NP-complete problem of determining if a clique can exist in the graph based if people are allies or enemies of each other

Let G (NP behavior) = the set of all people in the graph: {X_npi, X_npi+1, … X_npn}
where X_npi is one of the decisions in the problem that has NP behavior. G has NP behavior because all nodes in the graph must be examined while solving the problem to determine if cliques exist in the graph based if people are allies or enemies of each other.
Let Z (P behavior) = {ev_i, ev_i+1, … ev_a}
Let Z* (P behavior) = {ei_i, ei_i+1, … ei_c}
where i >=1 and i <= n.

The symmetric difference
S is the symmetric difference of Z and Z*
S = (Z \ Z*) U (Z* \ Z)
S = {ev_i, ev_i+1, … ev_a} \ {ei_i, ei_i+1, … ei_c} U {ei_i, ei_i+1, … ei_c} \ {ev_i, ev_i+1, … ev_a}
S = {ev_i, ev_i+1, … ev_a} U {ei_i, ei_i+1, … ei_c}
S = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c}
S = P behavior that includes both valid and invalid states.
where i >=1 and i <= n. ev_a is the last element in set Z where a is number of elements meaning decisions in set Z that have P behavior with valid states in the set Z. ei_c is the last element in set Z* where c is number of elements meaning decisions in set Z* that have P behavior with invalid states.
By Lemma 3 set S only contains P behavior.

Determining whether there is a clique in a graph
Let G (NP behavior) = the set of all people in the graph: {X_npi, X_npi+1, … X_npn}
where X_npi is one of the decisions in the problem that has NP behavior. G has NP behavior because all nodes in the graph must be examined while solving the problem to determine if cliques exist in the graph based if people are allies or enemies of each other.

Let Z = ALLIES IN THE k-PERSON CLIQUE (valid states)
Let Z = {ev_i, ev_i+1, … ev_a}
Let Z* = ENEMIES FORCED TO BE IN THE k-PERSON CLIQUE (invalid states)
Let Z* = {ei_i, ei_i+1, … ei_c}
where i >=1 and i <= n. ev_a is the last element in set Z where a is number of elements meaning decisions in set Z that have P behavior with valid states in the set Z. ei_c is the last element in set Z* where c is number of elements meaning decisions in set Z* that have P behavior with invalid states.

{ev_i, ev_i+1, … ev_a} represents decisions in the problem that have valid states, meaning people in the clique that are an ally, a valid state, of other people in the clique. Because it is known that {ev_i, ev_i+1, … ev_a} are allies, {ev_i, ev_i+1, … ev_a} have P behavior.

{ei_i, ei_i+1, … ei_c} represents decisions in the problem that have invalid states, meaning people in the clique that are an enemy, an invalid state, of other people in the clique. Because it is known that {ei_i, ei_i+1, … ei_c} are enemies, {ei_i, ei_i+1, … ei_c} have P behavior.

By Lemma 2, set Z* is the complement set of set Z because the elements in set Z* are the opposite of set Z but related to the same problem. By Lemma 3, the symmetric difference S of set Z and Z* has only P behavior.

S is the symmetric difference of Z and Z*
S = (Z \ Z*) U (Z* \ Z)
S = ({ev_i, ev_i+1, … ev_a} \ {ei_i, ei_i+1, … ei_c}) U ({ei_i, ei_i+1, … ei_c} \ {ev_i, ev_i+1, … ev_a})
S = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c}
where i >=1 and i <= n. ev_a is the last element in set Z where a is number of elements meaning decisions in set Z that have P behavior with valid states in the set Z. ei_c is the last element in set Z* where c is number of elements meaning decisions in set Z* that have P behavior with invalid states.

The key point
The symmetric difference S eliminates NP behavior by preventing ev_i and ei_i, an ally and an enemy, to be in the symmetric difference S whenever ev_i is the same as ei_i. This means the symmetric difference S prevents an element to be in the clique if an ally is also an enemy of another element in the clique. This is the case when ev_i = ei_i which occurs when ev_i and ei_i are in the intersection of set Z and set Z*. The symmetric difference of set Z and set Z* eliminates the intersection of set Z and Z*. This is why elements in the symmetric difference of set Z and set Z* can be in a clique. This property can be used to determine what elements can be in a k-person clique in deterministic polynomial time.

Let S = {{ev_i, ei_i} ∈ {(Z \ Z) U (Z \ Z)} : ev_i ≠ ei_i}
Then NP behavior is eliminated from S and only P behavior remains in S.

By Corollary 1, invalid states can be removed from the symmetric difference in deterministic polynomial time, linear time O(n), so the set of desired states contains only valid states {ev_i, ev_i+1, … ev_a}.

Example of determining whether there is a clique in a graph
Let G = all people in the graph: X₁, X₂, X₃, X₄, X₅, X₆, X_i, X_i+1, … X_n
Let A = a set of allies of each other: X₃, X₄, X₅
Let E = a set of enemies of each other: X₁, X₄, X₅
Determine if the candidate clique {X₁, X₃, X₄} can exist with the sets of allies and enemies defined above.

Let Z = ALLIES IN THE k-PERSON CLIQUE (valid states): X₃, X₄
Let Z* = ENEMIES FORCED TO BE IN THE k-PERSON CLIQUE (invalid states): X₁, X₄

S is the symmetric difference of Z and Z*
S = (Z \ Z*) U (Z* \ Z)
S = ({X₃, X₄} \ {X₁, X₄}) U ({X₁, X₄} \ {X₃, X₄})
S = {X₃, X₁}) U ({X₁, X₃}
S = {X₁, X₃}

An element cannot be part of a clique in graph G when one of the following situations occurs:

1. An element in the candidate clique is in both the set Z of valid states and the set Z* of invalid states. The symmetric difference prevents this situation because an element with NP behavior, having both valid and invalid states, is removed from the symmetric difference S. In the example above, element X₄ has this property.
   
2. An element in the symmetric difference S, but the element does not have an ally in the candidate clique. An element cannot be part of the candidate clique if the element is not an ally of any other element in the candidate clique. This is the case with element X₁ in the example above.

Situation 2. still results in P behavior in the solution when Corollary 1 is used to detect and remove from the symmetric difference S elements with this property in linear time when a hash set or hash table is used.

By Corollary 1, elements that are not an ally of any other element in the candidate clique (invalid states in this context) can be removed from the symmetric difference in deterministic polynomial time, linear time O(n), so the set of desired states contains only valid states.
D = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c} – {elements not an ally of any other element in the candidate clique}
The element {X₁} is an invalid state because X₁ is not an ally of any other element in set G, the set of all people in the graph.
D = {X₁, X₃} – {X₁}
D = {X₃}

The symmetric difference S shows X₁ and X₃ can be in the candidate clique {X₁, X₃, X₄} but X₄ can’t be in the candidate clique {X₁, X₃, X₄} because X₁ and X₄ are enemies of each other.

The set of desired states D shows the element X₁ can’t be in the candidate clique {X₁, X₃, X₄} because X₁ is not an ally of any other element in the candidate clique.

Proof of Lemma 4, by construction.
Let G be a graph with n vertices representing people. A person can be either an ally or an enemy of another person.
Let G = all people in the graph = {X_npi, X_npi+1, … X_npn}
where i >=1 and i <= n and X_npi is one of the decisions in the problem that has NP behavior, meaning need to decide if the person X_npi in G is an ally or an enemy of another person in the clique.

Let A = a set of allies of each other: X_i, X_i+1, …, X_n

Let E = a set of enemies of each other: X_i, X_i+1, …, X_n

Wanted: check graph G if a k-person clique is possible in the candidate set C = {X_i, X_i+1, …, X_k} where k >= 1 and k <= n. Do this in O(k) time.

First, set up the complement sets

Z = valid states / allies
Z* = invalid states / enemies

NP behavior is reduced in the problem by identifying people who can and cannot be in the clique by creating a set Z represented by the complex number a + bi and set Z* represented by the conjugate a – bi. a + bi represents the graph reduced to the valid states of a clique, only allies are in the clique. The conjugate a – bi represents the graph reduced to the invalid states of a clique, enemies are forced to be in the clique.

Label the elements in set Z and set Z* in the following way where ev_i represents the result of making decision based on valid states (allies in the clique), and where ei_i represents the result of making decision based invalid states (enemies in the clique).

Z = ALLIES IN THE k-PERSON CLIQUE (valid states)
Z = {ev_i, ev_i+1, … ev_n}
Z* = ENEMIES FORCED TO BE IN THE k-PERSON CLIQUE (invalid states)
Z* = {ei_i, ei_i+1, … ei_n}
where i >=1 and i <= n.

The letter v in ev_i represents valid states, and the letter i in ei_i represents invalid states. Set Z is the set of decisions after the problem was reduced by using only valid states and set Z* is the set of decisions after the problem was reduced by using only invalid states. ev_a is the last element in set Z where a is number of elements meaning decisions in set Z that have P behavior with valid states in the set Z. ei_c is the last element in set Z* where c is number of elements meaning decisions in set Z* that have P behavior with invalid states.

The graph G has NP behavior because all nodes in the graph must be examined while solving the problem to determine if cliques exist in the graph based on whether people are allies or enemies of each other. By Lemma 2, Z is reduced because Z has P behavior. It is not needed to determine if elements in Z are allies or enemies of each other; it it known that Z contains people who are allies that are added to the candidate clique. By Lemma 2, Z* is reduced because Z* has P behavior and Z* is the complement of Z. It is not needed to determine if elements in Z* are allies or enemies of each other; it it known that Z* contains people who are enemies of each other who are forced to be in the candidate clique.

Next, calculate the symmetric difference of the complement sets

By Lemma 3, the symmetric difference S of Z and Z* results in only P behavior. Only elements from a set with P behavior can be added to the clique; otherwise, if elements from a set with NP behavior is added to the clique then all combinations from all of the elements will need to be examined to determined if an element can be added to the clique. Therefore, elements of the symmetric difference S of sets Z and Z* will contain P behavior so those elements in the symmetric difference can be in the clique since all combinations from all those elements will not need to be examined. If elements {X_i, X_i+1, …, X_n} where i >= 1 and i <= n are not defined to be either allies or enemies of each other, then those elements have NP behavior so those elements will not be in the symmetric difference so they will not be members of a clique in the graph.

Next, find the intersection of the complement sets

To solve the nondeterministic polynomial problem in polynomial time, the intersection of the complex number and its conjugate is the NP behavior in the problem that must be avoided when solving the problem and the symmetric difference of the complex number and its conjugate are the decisions in the problem that are made with P behavior when solving the problem. Avoiding decisions in the intersection of Z and Z* will allow a nondeterministic polynomial problem to be solved in deterministic polynomial time.

Determining if a decision is in the intersection of Z and Z* can be quickly determined in constant time O(1) by using an XOR operation from the lookup result of a hash table or hash set. A decision in the intersection of Z and Z* has NP behavior so determining in constant time if a decision has NP behavior will also result in determining in constant time if a decision is in the symmetric difference of set Z and set Z*, meaning if the decision can solve a problem in P time by using an XOR operation from the lookup result of a hash table or hash set. Elements in the symmetric difference of set Z and set Z* can be used to solve the problem in deterministic polynomial time. This is how a nondeterministic polynomial problem can be both verified and solved in deterministic polynomial time.

An element is in the symmetric difference of set Z and set Z* if the element is in either of the sets, but not both and not in neither.

Check the construction for this proof by using hash sets named setZ and setZ* with the example above:

Let G = all people in the graph: X₁, X₂, X₃, X₄, X₅, X₆, X_i, X_i+1, … X_n
Let A = a set of allies of each other: X₃, X₄, X₅
Let E = a set of enemies of each other: X₁, X₄, X₅
Determine if the candidate clique {X₁, X₃, X₄} can exist with the sets of allies and enemies defined above.

Let Z = ALLIES IN THE k-PERSON CLIQUE (valid states): X₃, X₄
Let Z* = ENEMIES FORCED TO BE IN THE k-PERSON CLIQUE (invalid states): X₁, X₄

S is the symmetric difference of Z and Z*
S = (Z \ Z*) U (Z* \ Z)
S = ({X₃, X₄} \ {X₁, X₄}) U ({X₁, X₄} \ {X₃, X₄})
S = {X₃, X₁}) U ({X₁, X₃}
S = {X₁, X₃}

setZ.Contains(X₁) XOR setZ*.Contains(X₁) = F XOR T = T X₁ can be in the candidate clique

setZ.Contains(X₂) XOR setZ*.Contains(X₂) = F XOR F = F not in either set

setZ.Contains(X₃) XOR setZ*.Contains(X₃) = T XOR F = T X₃ can be in the candidate clique

setZ.Contains(X₄) XOR setZ*.Contains(X₄) = T XOR T = F in both sets

setZ.Contains(X₅) XOR setZ*.Contains(X₅) = F XOR F = F not in either set

setZ.Contains({X_i, X_i+1, … X_n}) XOR setZ*.Contains({X_i, X_i+1, … X_n}) = F XOR F = F not in either set, where i >= 7

Because elements {X_i, X_i+1, … X_n} where i >= 7 are not defined to be either enemies or allies of each other, they have NP behavior so they cannot be members of a clique in the graph. This is why the symmetric difference of set Z and set Z* does not include the elements {X_i, X_i+1, … X_n}.

Therefore, it is possible that the elements in the symmetric difference S {X₁, X₃} can be in the candidate clique {X₁, X₃, X₄} but X₄ cannot.

Next, eliminate elements from the symmetric difference that do not have any allies in the candidate clique

An element cannot be part of a clique in graph G when one of the following situations occurs:

1. An element in the candidate clique is in both the set Z of valid states and the set Z* of invalid states. The symmetric difference prevents this situation because an element with NP behavior, having both valid and invalid states, is removed from the symmetric difference S. In the example above, element X₄ has this property.
   
2. An element in the symmetric difference S, but the element does not have an ally in the candidate clique. An element cannot be part of the candidate clique if the element is not an ally of any other element in the candidate clique. This is the case with element X₁ in the example above.

Situation 2. still results in P behavior in the solution when Corollary 1 is used to detect and remove from the symmetric difference S elements with this property in linear time when a hash set or hash table is used.

By Corollary 1, elements that are not an ally of any other element in the candidate clique (invalid states in this context) can be removed from the symmetric difference in deterministic polynomial time, linear time O(n), so the set of desired states contains only valid states.
D = {ev_i, ev_i+1, … ev_a, ei_i, ei_i+1, … ei_c} – {elements not an ally of any other element in the candidate clique}
The element {X₁} is an invalid state because X₁ is not an ally of any other element in set G, the set of all people in the graph.
D = {X₁, X₃} – {X₁}
D = {X₃}

The set of desired states D shows X₁ and X₃ can be in the candidate clique {X₁, X₃, X₄} but X₄ can’t be in the candidate clique {X₁, X₃, X₄} because X₁ and X₄ are enemies of each other. The element X₁ can’t be in the candidate clique {X₁, X₃, X₄} because X₁ is not an ally of any other element in the candidate clique.

To reiterate the steps in the proof, set up the complement sets, calculate the symmetric difference of the complement sets and remove elements with invalid states. In this context, invalid states are elements from the symmetric difference that are not an ally of any other element in the candidate clique.

Z = ALLIES IN THE k-PERSON CLIQUE (valid states)
Z* = ENEMIES FORCED TO BE IN THE k-PERSON CLIQUE (invalid states)
S = (Z \ Z*) U (Z* \ Z)
D = S – Z*
D = {evi, evi+1, … eva, ei_i, ei_i+1, … eic} – {elements that are not an ally of any other element in the candidate clique (invalid states in this context)}

When using an XOR operator, determining if the candidate clique can exist takes O(1 * k) = O(k) time where k is the number of vertices in the candidate clique and k >= 1 and k <= n and n is the number of vertices in the graph G.

By Lemma 1, adding any number of elements Xi to the graph G will still result in the set of decisions represented by the imaginary dimension of a complex number to contain only P behavior of the problem and the set of decisions represented by the real dimension of a complex number will contain NP behavior of the problem. Therefore, any number of elements Xi can be added to the clique problem and Lemma 1 will still be true. With Lemma 1 holding true, Lemma 2 and Lemma 3 will hold true. The problem of determining whether there is a clique in a graph can be solved in deterministic polynomial time, linear time O(n), where n is the number of vertices in the graph when complex numbers and the symmetric difference of the complement sets Z and Z* are used to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number). Therefore, Lemma 4 is proved.

Lemma 5
Lemma 4 prevents an element to have invalid direct relationships in a clique in a graph if an ally is also an enemy of another element in the clique, but Lemma 4 does not prevent invalid transitive relationships from being in the clique. However, the symmetric difference of complement sets only allows valid transitive relationships to be in the clique when the complement sets are the graph (Z) and the inverted graph (Z*). When complex numbers and complement sets are used to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number), the problem of determining valid transitive relationships in a graph is solved in deterministic polynomial time of O(V + E).

Proof of Lemma 5
By construction.

Let G = all people in the graph: X₁, X₂, X₃, X₄, X₅, X₆, X_i, X_i+1, … X_n
Let A = a set of valid edges of the allied relationships: (X₃ and X₄), (X₄ and X₅) based on the set of allies of each other: X₃, X₄, X₅
Let E = a set of enemies of each other: X₁, X₄, X₅

Let Z = a set of allied relationships: (X₃ and X₄), (X₄ and X₅)
Let Z* = The complement of Z, meaning the inverted graph of Z: (X₃ and X₅)

1. By Lemma 4, determining the maximum clique in a graph takes a maximum deterministic polynomial time of O(n).
2. Determine if only valid transitive relationships can exist in the clique found by using Lemma 4 by removing enemies E from the intersection I to prevent invalid transitive relationships from being in the clique. By Corollary 1, removing invalid states, the enemies in set E, from a set that does not contain NP behavior is done in deterministic polynomial time. The symmetric difference S and the complement set Z* both do not contain NP behavior. Set Z* = {(X₃ and X₅)}. By Corollary 1, removing enemies from Z* is done in deterministic polynomial time.
3. By Corollary 1, set D = Z* – E = {(X₃ and X₅)} – {X₁, X₄, X₅} = {(X₃ and X₅)}
4. Removing enemies E from the set Z* results in only valid transitive relationships {(X₃ and X₅)} to be in set D.
5. The intersection I of a graph and its complement (inverted) graph, Z and Z*, is the empty set {} because it’s not possible for a graph to be itself and another graph at the same time.
6. Set D is a subset of set Z* so it follows that the intersection I of Z and D is the empty set{}.
7. Therefore, there is no NP behavior left in the intersection I so by Lemma 3 the symmetric difference S of Z and D results in in only valid transitive relationships in a clique.

Removing invalid transitive relationships from a clique in a graph can now be solved in linear time O(V + E) where V = number of vertices in a graph, E = number of edges in a graph. Therefore, determining the maximum clique in a graph that has only valid transitive relationships takes a maximum deterministic polynomial time of O(V + E). Therefore, Lemma 5 is proved

Lemma 6
When complex numbers and complement sets are used to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number), the problem of determining the maximum clique in a graph, a clique with the largest possible number of vertices, is solved in deterministic polynomial time.

Proof of Lemma 6
By construction.
1. Given a graph G with n vertices.

2. By Lemma 2, reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number) using complex numbers and complement sets where the complex number a + bi, represented by set Z, contains valid states, and the conjugate a – bi, represented by set Z*, contains invalid states.

3. By Lemma 5, use the symmetric difference to find in deterministic polynomial time of O(V + E), where V = number of vertices in a graph, E = number of edges in a graph, the vertices in graph G that can be added to the clique. The number of elements in the symmetric difference is the maximum number of vertices that can be in the clique.

Step 3 requires a deterministic polynomial amount of time O(V + E). Therefore, determining the maximum clique in a graph takes a maximum deterministic polynomial time of O(V + E), where V = number of vertices in a graph, E = number of edges in a graph. Therefore, Lemma 6 is proved.

Theorem
When complex numbers and complement sets are used to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number), a nondeterministic polynomial decision problem can be solved in deterministic polynomial time and be proved in deterministic polynomial time. P = NP.

Proof of Theorem P = NP
By direct proof:
1. Stephen Cook’s theorem states any problem in NP can be reduced in polynomial time by a deterministic Turing machine to the Boolean satisfiability problem (SAT) and SAT is NP-complete.[2]
2. Stephen Cook’s theorem states SAT is NP-complete so all problems in NP are at least as difficult to solve as SAT.[2]
3. If there exists a deterministic polynomial time algorithm for solving SAT, then every problem in NP can be solved by a deterministic polynomial time algorithm.
4. Richard Karp showed any SAT problem can be reduced to 3SAT in polynomial time and SAT is NP-complete so 3SAT is also NP-complete.[3]
5. Richard Karp showed 3SAT is reduced in polynomial time to the clique problem.[3]
6. Richard Karp’s 21 NP-complete problems states the clique problem of finding the maximum clique in a graph is NP-complete.[3]
7. By Lemma 4, determining the maximum clique in a graph with valid transitive relationships can be solved in deterministic polynomial time O(V + E) when using complex numbers and the symmetric difference of complement sets to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number).
8. Since SAT is reduced to 3SAT and 3SAT is reduced to cliques[3], determining the maximum clique in a graph can be solved in deterministic polynomial time O(V + E) which follows that 3SAT and SAT can be solved in deterministic polynomial time when using complex numbers and the symmetric difference of complement sets to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number).
9. Since SAT can be solved in deterministic polynomial time when using complex numbers and the symmetric difference of complement sets to reduce a problem by replacing a choice involving many decisions (nondeterministic polynomial in number) with a choice that has only one decision (deterministic polynomial in number), it follows that all NP problems can be solved in deterministic polynomial time.
10. Thus, P = NP [4]

Why P = NP, not P != NP
If the axes of the complex number a + bi were switched so the real dimension represents the P behavior of the problem and the imaginary dimension represents the NP behavior of the problem, then before a problem is reduced, which is when i = 0, it would mean the NP problem was already reduced before it was reduced which is not possible.

APPLICATIONS OF P = NP

FINDING CONTRADICTIONS IN SYSTEMS THAT OPERATE FOR EXTENDED PERIODS OF TIME

The halting problem / undecidability
According to the Halting problem, it is not possible to design a generalized algorithm that determines if a given problem halts or not. However, the P = NP proof in this paper provides a way to answer the halting problem if the halting problem is interpreted as asking, “Can a conclusion be reasoned from the premises? Is there a Yes or No answer to the problem?” The P = NP proof in this paper provides a way to detect logical contradictions (inconsistencies) in the premises of an algorithm by:
1. Setting up the complement sets Z and Z* where
2. By Lemma 1, Z = the polynomial-time reduction of the premises which causes the set of decisions represented by the imaginary dimension of a complex number to result in only P behavior of the problem to be added to the imaginary dimension of the complex number.
3. By Lemma 2, Z* = the complement set of the polynomial-time reduction of the premises.
4. The intersection of Z and Z* are the contradictions that prevent a problem from being solved or halted. By Lemma 4, NP behavior is the condition where ev_i = ei_i. Because the element in the intersection is both valid and invalid, it is a contradiction. Likewise, for the halting problem, if (Z XOR Z*) = (T XOR T) = False, then there are contradictions in the premises so the program is not solvable and it will never halt. If (Z XOR Z*) = True, then there are no contradictions in the premises so the program is solvable and it will halt.

The halting problem HP is defined as
HP = {(M) | M is a Turing Machine that halts on input(M)} [1]
To make HP decidable, contradictions in the premises of an algorithm must be detected. To do this, determine when the Turing Machine M will halt by setting up the complement sets Z and Z*. Define the language L(M) and L(M*) as
Z = L(M) = {(M) | M is a Turing Machine constructed from the set Z}
Z* = L(M*) = {(M*) | M* is a Turing Machine constructed from the complement set Z*}. By Lemma 4, NP behavior is the condition where ev_i = ei_i. An the element in the intersection is both valid and invalid so it is a contradiction. Likewise, for the halting problem, if (L(M) XOR L(M*)) = (T XOR T) = False, then there are contradictions in the premises so the Turing Machine M is not solvable and it will never halt. If (L(M) XOR L(M*)) = True, then there are no contradictions in the premises so the Turing Machine M is solvable and it will halt.

Check using the definition of a Turing Machine

Γ = finite alphabet, ∑ = input alphabet. A Configuration of M is the string xqy with x,y ∈ Γ, where y is not the empty string and q ∈ Q, where Q = set of the possible states q0, qaccept, qreject. [1]

The computation of M on input w ∈ ∑ is the unique sequence C0, C1,… of configurations such that C0 = q0w (or C0 = q0b if w is empty) and Ci goes to the next Turing Machine configuration Ci+1 for each i with Ci+1 in the computation and either the sequence is infinite or it ends in a halting configuration. If the computation is finite, then the number of steps is one less than the number of configurations and the finite configuration contains the state qaccept; otherwise, the number of steps is infinite.

A configuration examines valid and invalid states.

Z = examines only valid steps which is less than the number of both valid and invalid steps. The number of configurations in Z is less than the number of configurations in the original problem before it was reduced to Z.
Z* = examines only invalid steps which is less than the number of both valid and invalid steps. The number of configurations in Z* is less than the number of configurations in the original problem before it was reduced to Z*.

=> Z and Z* are both finite since they both contain less than the number of configurations in the original problem and the final configuration contains the state qaccept when (Z XOR Z*) = T. Because (Z XOR Z*) is only T when there are no contradictions this allows a problem to be determined if it halts, meaning it is solvable.

Therefore M and M* are finite and M and M* accept input w (w ∈ ∑) so the computation halts when (Z XOR Z*) = T.

Example of detecting infinite loops in software: contradictions that prevent halting

How to find the contradictions:
x = InitialValue
while Condition
begin
Change_in_x
end

Set up the complement sets Z and Z*

Premise #1: Initially x = InitialValue
Premise #2: Condition: the polynomial-time reduction of the premises
Premise #3: Change_in_x
Z = Condition AND Change_in_x

Z* = Opposite_of_condition OR Opposite_change_in_x

If (Z XOR Z*) = (T XOR T) = F, then there are contradictions in the premises so the algorithm is not solvable and it will not halt.

If (Z XOR Z*) = T, then there are no contradictions in the premises so the algorithm is solvable and it will halt.

Example 1 – Given the following code:

x = 100

while x < 200

begin

x = x – 1

end

Set up the complement sets Z and Z*

Premise #1: Initially x = 100
Premise #2: x < 200 (the polynomial-time reduction of the premises)

Premise #3: x = x – 1 (x = x – 1 means minus infinity)

Z = x < 200 AND x = x – 1

Z* = x >= 200 OR x = x + 1 (x = x + 1 means positive infinity)

For Z, It is possible for 100 (Premise #1) to be < 200 (Premise #2) AND for x to have values decreasing down to negative infinity (Premise #3) {negative infinity,…,98, 99, 100}, Z evaluates to True.
For Z*, it is possible for values not 100 (complement of Premise #1) to be >= 200 (complement of Premise #2) OR for x to have values increasing up to positive infinity (complement of Premise #3): {200, 201, …, positive infinity}, Z* evaluates to True
Because (Z XOR Z*) = (T XOR T) = F, there are contradictions in the premises so the algorithm is not solvable and it will not halt.

Example 2 – Given the following code:
x = 100

while x > 200

begin

x = x – 1

end
Set up the complement sets Z and Z*
Premise #1: Initially x = 100
Premise #2: x > 200 (the polynomial-time reduction of the premises)
Premise #3: x = x – 1 (x = x – 1 means minus infinity)
Z = x > 200 AND x = x – 1

Z* = x <= 200 OR x = x + 1 (x = x + 1 means positive infinity)

For Z, It is not possible for 100 (Premise #1) to be > 200 (Premise #2) AND for x to have values decreasing down to negative infinity (Premise #3), Z evaluates to False.
For Z*, it is possible for values not 100 (complement of Premise #1) to be <= 200 (complement of Premise #2) OR for x to have values increasing (complement of Premise #3) until complement of Premise #2 is reached {101, 102, …, 200}, so Z* evaluates to True.
Because (Z XOR Z*) = (F XOR T) = T, there are no contradictions in the premises so the algorithm is solvable and it will halt.

Completeness
The question: Is there a way to prove every true statement has a proof?
Answer:
1. If A then B is equivalent to (not A) or B
2. Set up the complement sets Z and Z* where
3. By Lemma 1, Z = the boolean logic of the premise.
4. By Lemma 2, Z* = the complement of the boolean logic of the premise.
5. The intersection of Z and Z* are the contradictions that prevent a premise from being proved. By Lemma 4, NP behavior is the condition where evi = eii. Because the element in the intersection is both valid and invalid, it is a contradiction. Likewise, for the completeness problem, if (Z XOR Z*) = (T XOR T) = False, then there are contradictions in the premises so the premise cannot be true and the premises cannot be proved. If (Z XOR Z*) = True, then there are no contradictions so the premise is true and can be proved.

Consistency
The question: Is a mathematical system free of contradictions?
Answer: can’t prove (A and not A) at the same time
The P = NP proof in this paper provides a way to answer the consistency problem if the consistency problem is interpreted as asking, “Can a conclusion be reasoned from the premises? Is there a Yes or No answer to the problem?” The P = NP proof in this paper provides a way to detect logical contradictions (inconsistencies) in the premises of an algorithm by:
1. Setting up the complement sets Z and Z* where
2. By Lemma 1, Z = the polynomial-time reduction of the premises which causes the set of decisions represented by the imaginary dimension of a complex number to result in only P behavior of the problem to be added to the imaginary dimension of the complex number.
3. By Lemma 2, Z* = the complement set of the polynomial-time reduction of the premises.
4. The intersection of Z and Z* are the contradictions that prevent a problem from being consistent. By Lemma 4, NP behavior is the condition where evi = eii. Because the element in the intersection is both valid and invalid, it is a contradiction. Likewise, for the consistency problem, if (Z XOR Z*) = (T XOR T) = False, then there are contradictions in the premises so the mathematical system is inconsistent. If (Z XOR Z*) = True, then there are no contradictions in the premises so the mathematical system is consistent.
Z = h, Z* = h+
Ego A Turing Machine can’t be itself (Z=T) and another Turing machine (Z*=T) at the same time (T XOR T = F). Therefore, the Turing Machine Z* = h+ cannot exist. Conclusion: The Turing Machine (h+) is inconsistent with itself (h); therefore, it is invalid.

Deadlock detection: preventing software from crashing (hanging)
The P = NP proof in this paper provides a way to detect deadlocks when acquiring resources in O(n) linear time, instead of examining all combinations of acquisitions in O(2^n) time, by:
1. Setting up the complement sets Z and Z*
2. Z = threads that are trying to acquire a lock
3. Z* = threads that have acquired a lock acquired by other threads
4. The intersection of Z and Z* are the threads that would cause a deadlock if they succeeded in acquiring the locks they need. By Lemma 4, NP behavior is the condition where ev_i = ei_i. Because the element in the intersection is both valid and invalid, it is a contradiction. Likewise, for deadlocks: If (Z XOR Z*) = (T XOR T) = False, then there are contradictions in the state of the software so the program is not solvable and it will never halt, meaning a deadlock occurs. If (Z XOR Z*) = True, then there are no contradictions in the state of the software so the program is solvable and it will halt, meaning a deadlock does not occur.

Example of a situation with three threads and three locks.
Thread 1 acquired Lock A
Thread 2 acquired Lock B
Thread 1 is blocked trying to acquire lock B

Let Z = Threads trying to acquire a lock (valid states)
Let Z* = Threads that have acquired a lock acquired by other threads (invalid states)

Z = {} No other thread is trying to acquire a lock
Z* = {Thread 1, Thread 2}

Because the intersection of Z and Z* is the empty set {}, a deadlock does not currently exist because Thread 2 is not blocked so it can release the lock that Thread 1 needs.

However, if Thread 3 attempts to acquire lock C then:

Thread 1 acquired Lock A
Thread 2 acquired Lock B
Thread 3 acquired Lock C
Thread 1 is blocked trying to acquire lock B
Thread 2 is blocked trying to acquire lock C
Thread 3 will be blocked if it acquired lock A

Let Z = Threads trying to acquire a lock (valid states)
Let Z* = Threads that have acquired a lock acquired by other threads (invalid states)

Z = {Thread 3}
Z* = {Thread 1, Thread 2,Thread 3}

Z.Exists(Thread 3) XOR Z*.Exists(Thread 3) = T XOR T = False Because the intersection of Z and Z ({Thread 3}) is not the empty set {}, a deadlock will occur if Thread 3 acquired lock A because all of the threads will be blocked waiting for the other threads to release their locks.

To prevent software from crashing (hanging), have a background thread or process either:
1. Detect when a crash has occurred. Constantly check when the intersection of Z and Z* is not the empty set {}. The intersection contains elements that have both valid and invalid states that caused the software to crash. In this worst case situation, restart the software to prevent the system from becoming non operational.
2. Prevent a crash from occurring. Constantly monitor the current state of the software to determine if the state of the software could cause the intersection of Z and Z* to not be the empty set {}. The intersection contains elements that have both valid and invalid states that could cause the software to crash. In this situation, prevent the system from crashing (hanging) by preventing the thread in the intersection of Z and Z* from acquiring the lock.

If a hash set or hash table is used, deadlocks can be detected in the intersection of Z and Z* in linear time O(n).

FINDING CONTRADICTIONS IN SYSTEMS THAT DO NOT OPERATE FOR EXTENDED PERIODS OF TIME

Russell’s paradox

The assumption that any property may be used to form a set, without restriction, leads to paradoxes. One common example is Russell’s paradox: there is no set consisting of “all sets that do not contain themselves”. Thus consistent systems of naive set theory must include some limitations on the principles which can be used to form sets.

Let R be the set of all sets that are not members of themselves. If R is not a member of itself, then its definition entails that it is a member of itself; yet, if it is a member of itself, then it is not a member of itself, since it is the set of all sets that are not members of themselves. The resulting contradiction is Russell’s paradox.

R1 = Rule #1 – Any property may be used to form a set.
R2 = Rule #2 – By Rule #1, sets can contain sets.
R3 = Rule #3 – By Rule #1, sets can contain themselves.

Approach to resolving the contradiction:

• Use P = NP to eliminate the rule that leads to a contradiction in naive set theory.
• If R2 is interpreted as “something else” and R3 is interpreted as “itself” then R2 and R3 are complement sets because they are the opposite of each other but related to the same problem. Z = R2 and Z* = R3 therefore the intersection of Z and Z* is a contradiction because something can’t be itself and something else at the same time.
• If (Z XOR Z*) = (T XOR T) = False, then there are contradictions in the rules of set theory so the rules are not solvable so the rules are not true.
• If (Z XOR Z*) = True, then there are no contradictions in the rules of set theory so the rules are solvable so the rules are true.
• Intersection of Z and Z* = conditions where the rules for a foundational mathematics cause contradictions..
• Symmetric difference of Z and Z* = conditions where contradictions in the rules for a foundational mathematics do not exist.
• Will show that if both Rule #2 and Rule #3 are true then a contradiction exists. Use P = NP to prove that both Rule #2 and Rule #3 cannot be true at the same time, only Rule #2 can be true so Rule #3 must be false. Thus Russell’s paradox is resolved.

Show that EITHER R2 and R3 can be true, but not both at the same time.
Z = R2 XOR R3 = (sets of sets) XOR (sets can contain themselves)
Z* = (not R2) AND (not R3) = (no sets of sets) AND (sets can’t contain themselves)

Case 1: (R2=T, R3=T) Z XOR Z* = (T XOR T) XOR (F AND F) = F XOR F = F, contradictions in set theory when R2 and R3 are both true.
Case 2: (R2=T, R3=F) Z XOR Z* = (T XOR F) XOR (F AND T) = T XOR F = T, no contradictions in set theory when R2 is T and R3 is F.
Case 3: (R2=F, R3=T/F) Impossible for R2 to be False because that would cause R1 to be violated so it’s irrelevant if R3 is True or False.

Analysis:
Case 1: R2 and R3 cannot both be true.
Case 2: Set theory can only exist without contradictions if R2 is true and R3 is false.
Case 3: If R2 is false, then that would cause R1 to be violated so R2 cannot be false.
Therefore, for set theory to exist without contradictions, R2 must be true and R3 must be false.

If R1 did not exist, then the results would be inconclusive, but the existence of R1 eliminates Case 3.

Using P = NP to eliminate the rules that lead to a contradiction can be useful when examining existing or new foundational concepts in mathematical systems.

Edit distance
The edit distance problem requires decisions whether to insert, replace or delete each character in the two strings. This results in a nondeterministic polynomial problem, 3 choices, for each character. Using dynamic programming, the edit distance problem is solved in O((|A| * |B|)) where A, B are strings resulting in quadratic run time O(n^2).

To solve the edit distance problem in linear O(n) time, convert the problem to a decision problem and use the symmetric difference of complement sets.

Complement sets:  For strings that contain binary characters, 0 or 1, the strings A and B are related to each other but contain characters that are complements of each other. Once the complement sets are defined, the symmetric difference of the complement of A and complement of B can be used to solve the edit distance problem because the symmetric difference of complement sets gets rid of the NP decisions, leaving only P decisions.

Z = string A
Z* = string B

Example 1
A:  111
B:  110
If the characters are binary, 0 or 1, then the complement of 0 is 1 and 1^c is 0.
Complement A (A^c):  000
Complement B (B^c):  001
Edit distance = intersection of A^c and B^c = {00} = Length(A,B) – Length(intersection of A^c and B^c) = 3 – 2 = 1
=> Determine that the edit distance of A and B = 1 in linear time O(n)

Example 2
A:  110   A^c:  001
B:  010   B^c:  101
Edit distance = Length(A,B) – Length(intersection of A^c and B^c) = 3 – 2 = 1

Example 3
A:  111   A^c:  000
B:  111   B^c:  000
Edit distance = Length(A,B) – Length(intersection of A^c and B^c) = 3 – 3 = 0

Example 4
For characters in the string that are not binary, define the complement of the characters.
For example, in this example with the characters being only {a, b, c, d}:
define 9 as complement of a
define 8 as complement as b
define 7 as complement as c
define 1 as complement of d

A:  abca   A^c:  9879
B:  dbc   B^c:  187
Edit distance = Length(max(A,B)) – Length(intersection of A^c and B^c) = 4 – 2 = 2

The NP-Complete graph isomorphism problem
Someone who has a conflicting sense of self, different egos, at the same time is a contradiction. Graph data structures, like code, has human characteristics. Finding conflicting egos in two graphs determines if the two graphs do not have the same shape.

The intersection of a graph and its complement graph, meaning the inverted graph, is the empty set because it’s not possible for a graph to be itself and another graph at the same time. So if the intersection of a graph and another graph’s complement is not the empty set, then a contradiction exists because the two graphs are the same and not the same at the same time.

By Lemma 6, to solve the graph isomorphism problem in linear time, O(V + E) time where V = number of vertices in a graph and E = number of edges in a graph, find the intersection of the first graph and the complement of the second graph because intersection I of a graph and its complement (inverted) graph, Z and Z*, is the empty set {} because it’s not possible for a graph to be itself and another graph at the same time. If the intersection I of a graph and another graph is the empty set, then the graphs are the same shape. If their intersection is not the empty set, then the graphs do not have the same shape.

The graph isomorphism problem can now be solved in linear time O(V + E) where V = number of vertices in a graph, E = number of edges in a graph..

REFERENCES